Assignment on Simple Linear Regression
EMBA Final Exam B01.1305
12 May 2021
• Please write your name on every answer book that you use. Make sure that you number your solutions correctly.
• Read all questions carefully.
• Show your work so that partial credit can be given. Poorly described solutions will be penalized.
• All questions are not of the same level of difficulty.
• For all multiple choice questions, one point for the right choice, the remaining points for justification.
• There are 4questions on this exam. You must complete all 4questions correctly to get full points (i.e.50 points) on this exam. Good Luck!
Name: ______________________________________________________________
1) [16 points] Answer the following questions. Justify your answers briefly. No credit will be given if you merely provide a choice without some justification for it.
a)[4 points]Your colleague in a financial institution says that she has been tracking the movements of the monthly returns of Facebook and Amazon stock returns. Using data on these returns over the last 10 years, she says that she has computed the COVARIANCE between these two return series and found that it is 0.00042. Since this COVARIANCE is so low and close to zero, she says that there does not seem to be any association between the two return series.
You tell her that (choose one of the following)
(i) her reasoning is faulty because….(give a brief reason)
(ii) her reasoning is correct because…(give a brief reason)
Her reasoning is faulty. Covariance can not be compared directly as it is unbounded and hence, the absolute value of covariance gives very little information. She should have calculated correlation which is covariance adjusted by the variance and then tested for significance to conclude anything.
correlation=b) [4 points] Is it possible that when you fit a simple regression model, the t-statistic for the slope coefficient is large (outside the range of (-2,2)), indicating that the X variable has a linear relationship with the Y variable, but that the R-squared value is quite low, say 8%?
(i) Yes (justify your choice with a short explanation)
(ii) No (justify your choice with a short explanation)
i. Yes. It may happen as the R-squared is the amount of variance explained. If the error or noise in the data is high, it can lead to low R-squared.
c) [4 points]Your colleague is running a simple regression of Y on X. He makes a plot of the standardized residuals vs. the fitted values shown below and you observe that there is a funnel
shape and so very clear evidence that there is non-constant variance in the data.
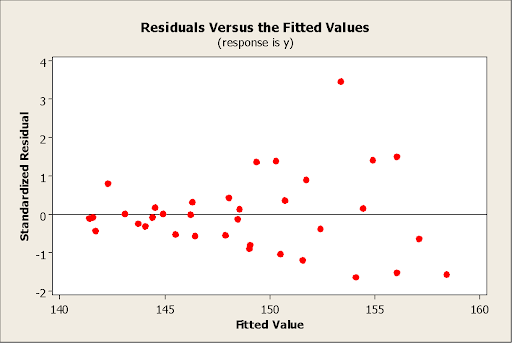
However, your colleague insists on going ahead and fitting the regression model without replacing the Y values with log(Y). Briefly yet clearly, describe the two errors that his resulting analysis, based on the untransformed Y variable, is likely to make.
The errors his analysis is likely to make are:
While heteroscedasticity does not cause bias in the coefficient estimates, it does make them less precise. Lower precision increases the likelihood that the coefficient estimates are further from the correct population value.
Heteroscedasticity tends to produce p-values that are smaller than they should be. This effect occurs because heteroscedasticity increases the variance of the coefficient estimates but the OLS procedure does not detect this increase.
d) [4 points]The regression of log(revenue of a firm) on log(R&D expenditure of firm) yields the following equation:
Log(Revenue) = 1.3 + 0.65 Log(R&D Expenditure)
In one sentence, interpret the value 0.65 of the slope in terms of the original variables “revenue of a firm” and “R&D expenditure of firm” (i.e. in terms of the unlogged variables)
Assuming natural log (i.e., base e log), the coefficient of 0.65 means that for each unit increase in R&D expenditure, the average increase in revenue is e^0.65=1.92 times.
2) [14 points] The marketing manager of a large supermarket chain would like to determine the effect of shelf space and whether the product was placed at the front or back of the aisle on the sales of pet food. A random sample of 12 equal-sized stores was taken and the following variables were noted:
Y= sales=daily sales of pet food (in thousands of $)
space=shelf space the per food in square feet
location=0 if the pet food was placed at the back of the aisle
= 1 if the pet food was placed at the front of the aisle
The output from the fitted multiple regression is shown below
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
| 0.213177 | 86.38% | 83.35% | 77.88% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
| Constant | 1.300 | 0.157 | 8.29 | 0.000 | |
| space | 0.0740 | 0.0110 | 6.72 | 0.000 | 1.00 |
| location | 0.450 | 0.131 | 3.45 | 0.007 | 1.00 |
Regression Equation
sales = 1.300 + 0.0740 space + 0.450 location
(i) [3 points] The manager believes that for a fixed amount of shelf space, products placed at the front of the aisle sell more on average than products placed at the back. Is there evidence to support his belief? (Justify your answer with an appropriate number)
Yes. The data contains the evidence to support his claims as the t-test for the significance of the location is statistically significant and the coefficient for the front is positive means if every other factor remains the same, the front location is expected to have higher sales than the back location.
(ii) [1 point] Predict the daily sales of pet food if the product is placed at the front of the aisle and has 6 square feet of shelf space devoted to it.
Predicted sales = 1.300 + 0.0740 *6 + 0.450 *1=2.194K
Predicted sales = 1.300 + 0.0740 *6 + 0.450 *1=2.194
The probability is very low (p = 0.0001) that the daily sales are less than $1550.
= 0 if the product was placed at the front of the aisle
She uses her model to predict daily sales of pet food if the product is placed at the front of the aisle and has 6 square feet of shelf space devoted to it. (i.e. the same characteristics as in part (ii) above)
(i) In what way would her predicted value differ from the value you obtained in (ii) above?
The predicted value will not be different. However, the coefficients will vary. The intercept will now be equal to 1.3+0.450 and the coefficient of the X2 will be -0.450.
The predicted value remains the same.
(ii) What estimate would she get for the coefficient of location in her fitted regression equation?
The coefficients will be:
Intercept = 1.750
Coef X1 = 0.074
CoefX2 = -0.450
3) [10 points]A real estate company has collected data on the following variables for several houses in a suburb of NYC:
Price: the price of the house (in $)
Story: the number of stories the house has
Baths: the number of baths the house has
A multiple regression fit to the above variables gave the following:
Regression Analysis: Price versus Story, Baths
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
| 53098.7 | 42.71% | 41.49% | 38.60% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value |
| Constant | -44623 | 21492 | -2.08 | 0.041 |
| Story | 63097 | 41786 | 1.51 | 0.131 |
| Baths | 42669 | 30048 | 1.42 |
Regression Equation
Price = -44623 + 63097 Story + 42669 Bathsa) [2 points] Which of the explanatory variables in the model are important on an individual basis, after accounting for the other variables?
You must state a number (or numbers) based on which you give your answer
The most important variable is Story. This is based on the p-values of the t-test. The p-value for Story is lower than Baths which makes it more effective. (Although, both of them are not statistically significant.)
b) [4 points] (Answer this question using the output on the earlier page as is, regardless of whatever you may have concluded in (a) above) The company has a house in the suburb that it wishes to sell. This house is 2 stories tall and has 1 bath. Based on the FULL MODEL on the previous page, make a suggestion for what price the agency should list the house at such that the agency is neither underselling the house nor overpricing it significantly. It is fine if your answer is a range of values. YOU MUST PROVIDE JUSTIFICATION IN A FEW BRIEF SENTENCES FOR HOW YOU CAME UP WITH YOUR VALUE (OR RANGE OF VALUES)
Price = -44623 + 63097 Story + 42669 Baths
Price = -44623+63097×2+42669×1=124240.
The fitted value is $124,240 which is the suggested price.
If a range of values is required, a 95% Prediction interval is calculated as:
Lower Limit = 124,240 – 53098.7*1.96 = $ 20,166.55
Upper limit = 124,240 + 53098.7*1.96 = $ 228,313.5
The fitted value is suggested as the sale price as this is the expected value of the price of the property. But if that is not agreed price, a range of values given by the prediction interval captures the value of the property with 95% confidence.
c) [4 points] When the analyst who carried out the analysis presents the model to the real estate agents at the company, the one agent says “I am quite puzzled by this. The variable “baths” has a t-statistic value within (-2,2),but I would definitely expect the number of bathrooms a house has to be related to its price
Give a brief but clear response to the agent to that will clear up their confusion
Ans: The data indicates that number of bathrooms may have increasing relationship with the house price, but this variable is not able to explain significant proportion of the variation in the house price which must be related through a lot of factors as well as it may have some interaction effect with other variable. This analysis is not a proof of causation and hence, cannot be taken as such. More variables might be used to explain the trend in house prices and then this relationship can be captured better.
4) [10 points] This question builds on the airport security problem in question 2 from HW 3. The paragraph below, describing the setup, is identical to that in the HW.
In November 2001, just after the 9/11 attacks, the NYTimes published an article titled “A small dose of common sense would help Congress break the deadlock over airport security”. The article considered the different factors that could impact the quality of security screening at airports. One of the factors that it considered was the turnover rate (a measure of how quickly employees leave the job) of airport security personnel and its potential impact on how good the security screening was. The article mentioned a study that considered the turnover rate at 19 airports across the country and also the violations detected (per million passengers) at each of those airports; the article reported that the study found that a lower turnover rate (i.e. employees stay in their job for a longer period) was associated with a greater likelihood of detecting violations (i.e. a large number of violations detected per million passengers) and thus advocated for measures that would reduce the turnover rate in order to increase the quality of the security screening
The original article in the newspaper also had the data for these two variables across the 19 airports and you can find that data in the file AirportViol
Below is a scatter plot of the violations detected per million passengers (Y) versus the turnover rate (X), as well as the output from a simple regression model fit to the data
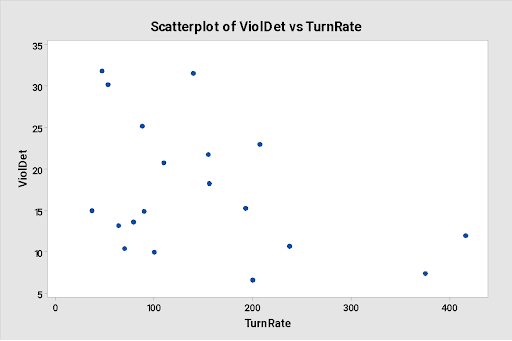
Regression Analysis: ViolDet versus TurnRate
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
| 7.50850 | 16.11% | 11.18% | 0.00% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
| Constant | 21.87 | 3.03 | 7.22 | 0.000 | |
| TurnRate | -0.0304 | 0.0168 | -1.81 | 0.088 | 1.00 |
Regression Equation
The sign of the estimated slope coefficient supports the argument that article made about the relationship between violations detected per million passengers and the turnover rate as the coefficient is negative. Negative coefficient indicate lower turn rate means higher violation detection.
Based on the regression output, is there evidence that there is a linear relationship between these two variables?
There is no evidence for a linear relationship based on the regression output at 5% level of significance. The t-test has t-value -1.81, p=.08 which is higher than 0.05.
The original NYTimes article (snapshot below; you do NOT have to read the article, I am just showing it for clarity) also provided the locations of each of the 19 airports for which the data had been collected.
Using this additional information on the location of each airport, I categorized the airports into one of two categories:
Airport in a major East or West coast city
Airport not in a major East or West coast city
I then created a dummy variable for “location in a major coastal city” to incorporate this information into the model, with the coding as
Coast = 1 if Airport in a major East or West coast city
=0 if Airport not in a major East or West coast city
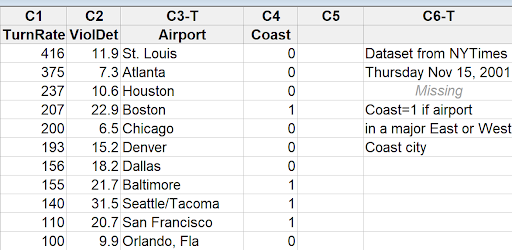
You can see the first few rows of the additional variable in the snapshot below:
Regression Analysis: ViolDet versus TurnRate, Coast
| S | R-sq | R-sq(adj) | R-sq(pred) |
| 5.47433 | 58.03% | 52.79% | 44.51% |
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
| Constant | 13.61 | 3.02 | 4.50 | 0.000 | |
| TurnRate | -0.0096 | 0.0133 | -0.72 | 0.483 | 1.18 |
| Coast | 10.92 | 2.73 | 4.00 | 0.001 | 1.18 |