Problem Description:
You are given a set of questions related to statistical analysis assignment and probability. Each question requires you to apply the Central Limit Theorem and various statistical methods to find probabilities and percentiles. Below are the solutions to each question.
Solution
Question 1
μ=30
σ=20
n=100
From the Central Limit Theorem, if a sample size is sufficiently large, n≥30, then the sample mean is approximately normally distributed with mean, μ_x ̿ =μ and standard deviation,
σ_x ̿ =σ/√n
Therefore, the sampling distribution of x ̅, has mean μ_x ̿ =30 and standard deviation,
σ_x ̿ =20/√100=2
Question 2
n=150
μ=240
σ=28
P(x ̿>4)=P(z>(239-240)/(28/√150))
=P(z>(-1)/2.28619)
=P(z>-0.4374)
=1-P(z<-0.4374)
=1-0.3309
=0.6691
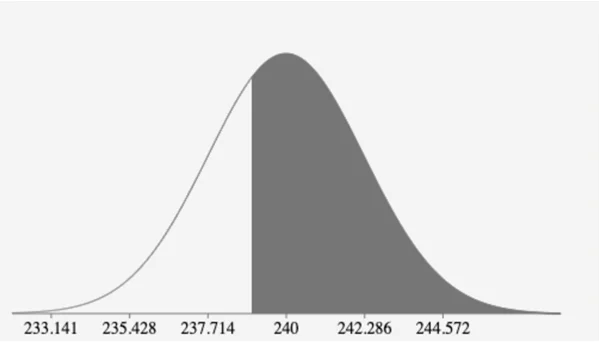
Question 2b
38th Percentile of the population
38/100=ϕ((x ̿-240)/(28/√150))
⟹ϕ^(-1) (0.38)=(x-240)/2.28619
⟹-0.305×2.28619=x-240
∴-0.6984=x-240
x=240-0.6984
=239.30
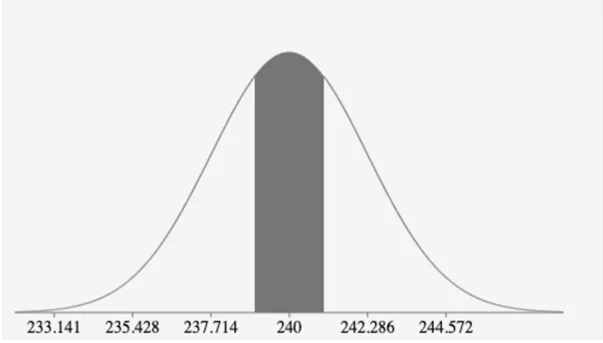
Question 2c
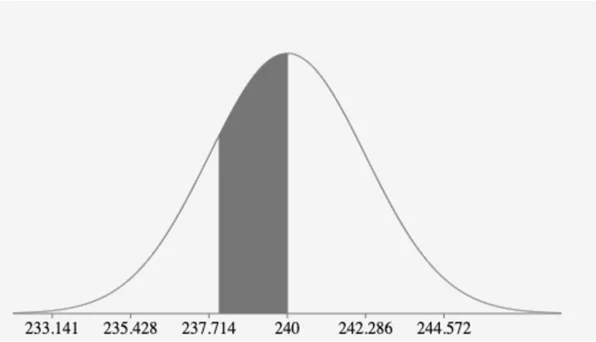
P(239
=P(-0.4374
=P(z<0.4374)-P(z<-0.4374)
=0.6691-0.3309
=0.3382
Question 2d
P(x ̿>242)=P(z>(242-240)/(28/√150))
=P(z>2/2.28619)
=P(z>0.8748)
=1-P(z<0.8748)
=0.1908
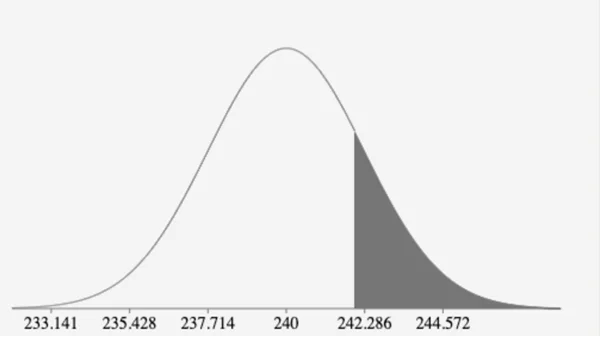
It is not unusual for the sample mean to be more than 242 since the calculated probability = 0.1908 is within the bounds of probability value; 0≤P≤1.
Question 2e
P(238
=P(-0.8748
=P(z<0)-P(z<-0.8748)
=0.5-0.1908
=0.3092
Question 3a
μ=2.25
σ=1.3
n=90
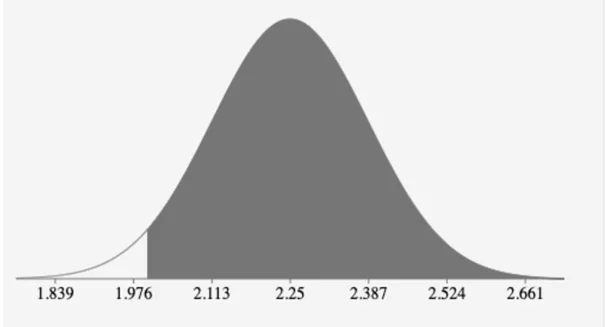
P(x ̿>2)=P(z>(2-2.25)/(1.3/√90))
=P(z>-1.8244)
=1-P(z<-1.8244)
=1-0.034
=0.966
Question 3b
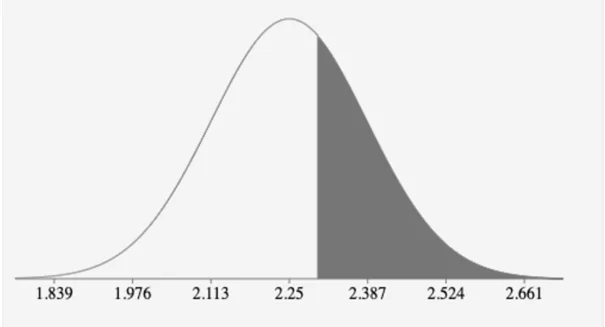
P(2.3
=P(0.3649
=P(z<6.9327)-P(z<0.3649)
=0.3576
Question 3c
20th Percentile of the population
20/100=ϕ((x ̿-2.25)/(1.3/√90))
⟹ϕ^(-1) (0.2)=(x-2.25)/0.1370
⟹-0.8416×0.1370=x-2.25
∴x=2.25-0.08870
=2.16
Question 3d
P(x ̿<2)=P(z<(2-2.25)/(1.3/√90))
=P(z<-1.8244)
=0.034
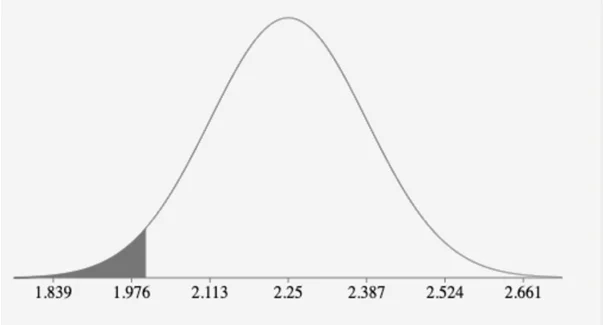
It would not be unusual for the sample mean to be less than 2 since the calculated probability =0.034 is within the bounds of probability value; 0≤P≤1.
Question 3e
P(x<2)=P(z<(2-2.25)/1.3)
=P(z<-0.1923)
=P(-0.1923)
=0.4238