Instructions
| (X) Weight (lbs) | (Y) Fuel Economy (mi/gal |
| 3466 | 21.5 |
| 2501 | 36.5 |
| 4731 | 19.0 |
| 3893 | 13.0 |
| 4925 | 19.5 |
| 3222 | 22.0 |
| 2899 | 46.0 |
A) Calculate the least squares line
B) Find the correlation coefficient r.
r=
C) Using the standard deviation for the residuals are there any data values that are more than 2 standard deviations above or below the least squares line?
Assignment Solution
| (X) Weight (lbs) | (Y) Fuel Economy (mi/gal |
| 3466 | 21.5 |
| 2501 | 36.5 |
| 4731 | 19.0 |
| 3893 | 13.0 |
| 4925 | 19.5 |
| 3222 | 22.0 |
| 2899 | 46.0 |
B) Calculate the least squares line
| (X) Weight (lbs) | (Y) Fuel Economy (mi/gal) | XY | X2 | Y2 |
| 3466 | 21.5 | 74519 | 12013156 | 462.25 |
| 2501 | 36.5 | 91286.5 | 6255001 | 1332.25 |
| 4731 | 19 | 89889 | 22382361 | 361 |
| 3893 | 13 | 50609 | 15155449 | 169 |
| 4925 | 19.5 | 96037.5 | 24255625 | 380.25 |
| 3222 | 22 | 70884 | 10381284 | 484 |
| 2899 | 46 | 133354 | 8404201 | 2116 |
| Σ=25637 | Σ=177.5 | Σ=606579 | Σ=98847077 | Σ=5304.75 |
Thus, Regression: y = bx+a = -0.0088*b + 57.52
C) Find the correlation coefficient r.
i) Using the standard deviation for the residuals are there any data values that are more than 2 standard deviations above or below the least squares line?
| (X) Weight (lbs) | (Y) Fuel Economy (mi/gal | yhat | y-yhat | res-mean | (res-mean)2 |
| 3466 | 21.5 | 27.09011 | -5.59011 | -5.58179 | 31.15638 |
| 2501 | 36.5 | 35.56281 | 0.93719 | 0.94551 | 0.893989 |
| 4731 | 19 | 15.98341 | 3.01659 | 3.02491 | 9.150081 |
| 3893 | 13 | 23.34105 | -10.3411 | -10.3327 | 106.7653 |
| 4925 | 19.5 | 14.28009 | 5.21991 | 5.22823 | 27.33439 |
| 3222 | 22 | 29.23243 | -7.23243 | -7.22411 | 52.18777 |
| 2899 | 46 | 32.06837 | 13.93163 | 13.93995 | 194.3222 |
| Mean=-0.00832 | Σ= 421.8101 |
SD for residuals =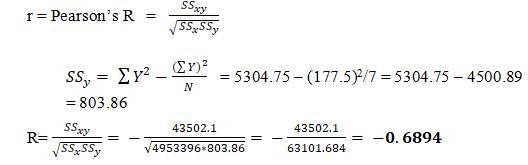
=8.3846
=8.3846Using this value of the standard deviation of residuals, the points below and above two standard deviations from the least square line are calculated below:
| (X) Weight (lbs) | (Y) Fuel Economy (mi/gal) | yhat | yhat-2*SD | Yhat+2*SD |
| 3466 | 21.5 | 27.09011 | 10.32089 | 43.85933 |
| 2501 | 36.5 | 35.56281 | 18.79359 | 52.33203 |
| 4731 | 19 | 15.98341 | -0.78581 | 32.75263 |
| 3893 | 13 | 23.34105 | 6.57183 | 40.11027 |
| 4925 | 19.5 | 14.28009 | -2.48913 | 31.04931 |
| 3222 | 22 | 29.23243 | 12.46321 | 46.00165 |
| 2899 | 46 | 32.06837 | 15.29915 | 48.83759 |
It can be seen that all the data values lie between below and above two standard deviations from the least square line.